Data Warehousing Fundamentals in Microstrategy

Data Warehousing Fundamentals in Microstrategy

A fundamental concept of a data warehouse is the distinction between data and information. Data is composed of observable and recordable facts that are often found in operational or transactional systems. In a data warehouse environment, data only comes to have value to end-users when it is organized and presented as information. Information is an integrated collection of facts and is used as the basis for decision-making.

Table of Contents Operational vs Decision-Support Systems  DWH Definition Time variant Data Data Granularity Top-Down Approach Bottom-Up Approach Data Marts Difference between Data Warehouse & OLTP Types of OLAPS Inside the Fact Table The Factless Fact Table Types of Facts Difference between Star and Snow Flake schema

Need for Data warehousing

• Companies are desperate for strategic information to counter fiercer competition, extend market share, and improve profitability.
• Despite tons of data accumulated by enterprises over the past decades, every enterprise is caught in the middle of an information crisis. Information needed for strategic decision making is not readily available.
• All the past attempts by IT to provide strategic information have been failures. This was mainly because IT has been trying to provide strategic information from operational systems.
• Informational systems are different from traditional operational systems. Operational systems are not designed for strategic information.
• We need a new type of computing environment to provide strategic information. The data warehouse promises to be this new computing environment.

Operational vs Decision-Support Systems

DWH is the solution for Strategic Business decisions

Strategic information is not for running the day-to-day operations of the business. It is not intended to produce an invoice, make a shipment, settle a claim or post-withdrawal from a bank account. Strategic information is far more important for the continued health and survival of the corporation. Critical business decisions depend on the availability of proper strategic information in an enterprise.

Desired Features for DWHing

The desired features of the new type of system environment are: o Database designed for analytical tasks

• Data from multiple applications
• Easy to use and conducive to long interactive sessions by users o Read-intensive data usage
• Direct interaction with the system by the users without IT assistance o Content updated periodically and stable
• Content to include current and historical data
• The ability for users to run queries and get results online o Ability for users to initiate reports

Want to acquire industry skills and gain complete knowledge of MicroStrategy? Enroll in Instructor-Led live MicroStrategy Training to become Job Ready!

DWH Definition

Bill Inmon considered to be the father of Data Warehousing provides the following definition:

“A Data Warehouse is a subject-oriented, integrated, non-volatile, and time-variant collection of data in support of management’s decisions.”Sean Kelly, another leading data warehousing practitioner defines the data warehouse in the following way.

The data in the data warehouse is:

• Separate
• Available
• Integrated
• Time-stamped
• Subject oriented

Integrated

Time variant Data

The time-variant nature of the data in a data warehouse

• Allows for analysis of the past
• Relates information to the present
• Enables forecasts for the future

Non-volatile Data

Every business transaction does not update the data in the data warehouse. The business transactions update the operational system databases in real-time. We add, change, or delete data from an operational system as each transaction happens but do not usually update the data in the data warehouse. You do not delete the data in the data warehouse in real-time. Once the data is captured in the data warehouse, you do not run individual transactions to change the data there. Data updates are commonplace in an operational database; not so in a data warehouse. The data in a data warehouse is not as volatile as the data in an operational database is. The data in a data warehouse is primarily for query and analysis.

Data Granularity

Data granularity in a data warehouse refers to the level of detail. The lower the level of detail, the finer the data granularity.

Data warehouse Approaches

Top-Down Approach

The advantages of this approach are:

• A truly corporate effort, an enterprise view of data
• Inherently architected—not a union of disparate data marts o Single, central storage of data about the content
• Centralized rules and control
• May see quick results if implemented with iterations

The disadvantages of this approach are:

• Takes longer to build even with an iterative method o High exposure/risk to failure
• Needs high level of cross-functional skills o High outlay without proof of concept

Read these latest MicroStrategy Advanced Interview Questions that help you grab high-paying jobs

Bottom-Up Approach

The advantages of this approach are:

• Faster and easier implementation of manageable pieces o Favorable return on investment and proof of concept o Less risk of failure
• Inherently incremental; can schedule important data marts first o Allows project team to learn and grow

The disadvantages of this approach are:

• Each data mart has its own narrow view of data o Permeates redundant data in every data mart o Perpetuates inconsistent and irreconcilable data
• Proliferates unmanageable interfaces

Data Marts

A data structure that is optimized for access. It is designed to facilitate end-user analysis of data. It typically supports a single, analytic application used by a distinct set of workers.

DATA MARTS: It is a collection of attributes that defines a specific business functionality (or) Tasks (or) Business.

Datamart Types:

• Dependent - After Warehouse is created data mart will be constructed.
• Independent - It is directly created from individual source systems.
• Logical - It is a replica of a dependent data mart.

Note: In Real, Time views are called as Datamarts.

DWH Life Cycle:

Requirements gathering & analysis.

Data or dimensional modeling

ETL

• Design
• Creation
• Test
• Load

Data Mart/ Creation Cube.

Reports

• Design
• Creation
• Test
• Implementation

Deployment

Warranty period/according to SLA(Service Level Agreement)

Maintenance support

Difference between Data Warehouse & OLTP:

OLTP	DWH
Designed for transaction processing	Designed for Decision support
Volatile	Store Non-volatile
Store current data only	Store historical data
Store detail data	Store summarized data
More joins	Less joins
Normalized	De-normalized
Fewer indexes	More indexes

Types of OLAPS

ROLAP (Relational OLAP): Applied on relational sources, both data and aggregate information stored and relational sources.

Ex: BO, Cogno’s, Crystal reports, MicroStrategy

MOLAP (Multidimensional OLAP): Here, Analysis will be done on multi-dimensional applications. Here, data and aggregate information stored under multidimensional sources.

HOLAP (Hybrid OLAP): Here data stored in relational sources and aggregated values under multidimensional sources “cubes”.

Ex: Cognos, BO, MicroStrategy

DOLAP (Desktop OLAP): Here, the analysis will be done on desktop Ex: MS-access, Excel, etc..

ETL [Extract Transform Load]:

• Extract: getting data from various sources
• Transform: doing intermediate operations
• Load: leading to the decision.

Examples:
ETL Tools:	Informatica, Data Stage, SSIS, OWB, etc
DataBase:	Oracle, SQL Server, DB2, Informix, Sybase, Access, etc.
Flat Files:	XML files, Text files(.csu, .txt, .dat, out)
ERP Systems:	SAPR/3, People soft, J.D., Edward, BANN……….
Other files:	Tibco M2 files, Excel files, etc……
Channel files:	Mainframes, IMS, COBOL, DB2, etc…

Data Modelling

• Enable developers to create and maintain data models for the source systems and the data warehouse target databases. If necessary, data models may be created for the staging area.

Provide forward engineering capabilities to generate the database schema.

• Provide reverse engineering capabilities to generate the data model from the data dictionary entries of existing source databases.

• Provide dimensional modeling capabilities to data designers for creating STAR schemas.

Data Extraction

• Two primary extraction methods are available: bulk extraction for full refreshes and change-based replication for incremental loads.

• Tool choices depend on the following factors: source system platforms and databases, and available built-in extraction and duplication facilities in the source systems.

Data Transformation

Transform extracted data into appropriate formats and data structures.

Provide default values as specified.

• Major features include field splitting, consolidation, standardization, and reduplication.

Data Loading

• Load transformed and consolidated data in the form of load images into the data warehouse repository.

Some loaders generate primary keys for the tables being loaded.

• For load images available on the same RDBMS engine as the data warehouse, pre-coded procedures stored on the database itself may be used for loading.

Data Quality

• Assist in locating and correcting data errors.
• May be used on the data in the staging area or on the source systems directly. Help resolve data inconsistencies in load images.

Queries and Reports

• Allow users to produce canned, graphic-intensive, sophisticated reports. Help users to formulate and run queries.
• Two main classifications are report writers, report servers.

Online Analytical Processing (OLAP)

Allow users to run complex dimensional queries. Enable users to generate canned queries.

• Two categories of online analytical processing are multidimensional online analytical processing (MOLAP) and relational online analytical processing (ROLAP). MOLAP works with proprietary multidimensional databases that receive data feeds from the main data warehouse. ROLAP provides online analytical processing capabilities from the relational database of the data warehouse itself.

Information Delivery:

Your requirements definition document must contain the following requirements on information delivery to the users:

• Drill-down analysis
• Roll-up analysis
• Drill-through analysis
• Slicing and dicing analysis
• Ad hoc reports

Preliminary Data Cleansing: In this step, you verify the extracted data from each data source for any missing values in individual fields, supply default values, and perform basic edits. This is another step for the computing platform of the source system itself. However, in some data warehouses, this type of data cleansing happens after the data from all sources are reconciled and consolidated. In either case, the features and conditions of data from your source systems dictate when and where this step must be performed for your data warehouse.

DATA MODELING

Data Model: A data model is an abstraction of some aspect of the real Why do we need Data Model?

• Helps to visualize the business
• A model is a means of communication.
• Models help elicit and document requirements.
• Models reduce the cost of change.
• Model is the essence of DW architecture based on which DW will be

Levels of Modelling:

Conceptual modeling:

Describe data requirements from a business point of view without technical details

Logical modeling:

• Refine conceptual models

• Data structure-oriented, platform-independent

Physical modeling:

The detailed specification of what is physically implemented using specific technology

Conceptual Model:

• A conceptual model shows data through business eyes.
• All entities which have business meaning.
• Important relationships
• Few significant attributes in the entities.
• Few identifiers or candidate (PK candidates) keys.

Logical Model:

• Replaces many-to-many relationships with associative entities.
• Defines a full population of entity attributes.
• May use non-physical entities for domains and sub-types.
• Establishes entity identifiers.
• Has no specific for any RDBMS or configuration.
• ER Diagram > Key Based Modeling > Fully Attributed Model

Physical Model:

A Physical data model may include

• Indexes
• Views
• Alternate keys and other constraints
• Tablespaces and physical storage objects.

E­-R Modeling Versus Dimensional Modeling:

We are familiar with data modeling for operational or OLTP systems. We adopt the Entity-Relationship (E-R) modeling technique to create the data models for these systems. Figure 10-5 lists the characteristics of OLTP systems and shows why E-R modeling is suitable for OLTP systems.

We have so far discussed the basics of the dimensional model and find that this model is most suitable for modeling the data for the data warehouse. Let us recapitulate the characteristics of the data warehouse information and review how dimensional modeling is suitable for this purpose. Let us study Figure 10-6.

Design Decisions:

Before we proceed with designing the dimensional data model, let us quickly review some of the design decisions you have to make:

• Choosing the process: Selecting the subjects from the information packages for the first set of logical structures to be designed.
• Choosing the grain: Determining the level of detail for the data in the data structures.
• Identifying and confirming the dimensions: Choosing the business dimensions (such as product, market, time, etc.) to be included in the first set of structures and making sure that each particular data element in every business dimension is conformed to one another.
• Choosing the facts: Selecting the metrics or units of measurements (such as product sale units, dollar sales, dollar revenue, etc.) to be included in the first set of structures.
• Choosing the duration of the database: Determining how far back in time you should go for historical data.

Dimensions:

• It is a collection of attributes, which defines a specific business or functionality or task.
• Also called as ‘Master Table’.
• Mainly answers for Where, What, When, Who, & Whom.
• It doesn’t contain historical information.
• It has less volume of fresh data.
• Contains textual information.

5 Types of Dimensions:

• Confirmed dimension
• Junk dimension
• Degenerated dimension
• Role-playing dimension
• Slowly changing dimension

Note: other dimensions Dirty dimension etc…

Degenerated Dimension:

• The value will exist in the fact table, but it will be stripped off from the dimension table.
• Dimensions with no other place to go
• Stored in the fact table
• Are not facts
• Common examples include invoice numbers or order numbers

Confirmed Dimension:

 It is shared across multiple facts or data marts.

Advantages:

• Enables an incremental development approach
• Easier and cheaper to maintain
• Drastically reduces extraction and loading complexity
• Answers business questions that cross data marts
• Supports both centralized and distributed architectures

Junk Dimension:

Instead of having multiple small dimensions (which contain less volume of data), we can have a large dimension and where we will store the data. Generally, we will maintain all small dimensions of information in facts with flags.

These attributes represent the textual descriptions of the components within the business dimensions. Users will compose their queries using these descriptors.

• Attributes are not directly related: Frequently you will find that some of the attributes in a dimension table are not directly related to the other attributes in the table. For example, the package size is not directly related to product brand; nevertheless, package size and product brand could both be attributes of the product dimension table.
• Not normalized: The attributes in a dimension table are used over and over again in queries. An attribute is taken as a constraint in a query and applied directly to the metrics in the fact table. For efficient query performance, it is best if the query picks up an attribute from the dimension table and goes directly to the fact table and not through other intermediary tables. If you normalize the dimension table, you will be creating such intermediary tables and that will not be efficient. Therefore, a dimension table is flattened out, not normalized.
• Drilling down, rolling up: The attributes in a dimension table provide the ability to get to the details from higher levels of aggregation to lower levels of details. For example, the three attributes zip, city, and state form a hierarchy. You may get the total sales by state, then drill down to total sales by city, and then by zipping. Going the other way, you may first get the totals by zipping, and then roll up to totals by city and state.
• Multiple hierarchies: In the example of the customer dimension, there is a single hierarchy going up from individual customers to zipping, city, and state. But dimension tables often provide for multiple hierarchies, so that drilling down may be performed along any of the multiple hierarchies. Take for example a product dimension table for a department store. In this business, the marketing department may have its way of classifying the products into product categories and product departments. On the other hand, the accounting department may group the products differently into categories and product departments. So in this case, the product dimension table will have the attributes of marketing–product–category, marketing–product–department, finance–product–category, and finance–product–department.
• The fewer number of records: A dimension table typically has fewer number of records or rows than the fact table. A product dimension table for an automaker may have just 500 rows. On the other hand, the fact table may contain millions of rows.

Inside the Fact Table

Let us now get into a fact table and examine the components. Remember this is where we keep the measurements. We may keep the details at the lowest possible level. In the department store fact table for sales analysis, we may keep the units sold by individual transactions at the cashier’s checkout. Some fact tables may just contain summary data. These are called aggregate fact tables. The below Figure lists the characteristics of a fact table. Let us review these characteristics.

• Concatenated Key: A row in the fact table relates to a combination of rows from all the dimension tables. In this example of a fact table, you find quantity ordered as an attribute. Let us say the dimension tables are product, time, customer, and sales representative. For these dimension tables, assume that the lowest level in the dimension hierarchies is an individual product, a calendar date, a specific customer, and a single sales representative. Then a single row in the fact table must relate to a particular product, a specific calendar date, a specific customer, and an individual sales representative. This means the row in the fact table must be identified by the primary keys of these four dimension tables. Thus, the primary key of the fact table must be the concatenation of the primary keys of all the dimension tables.
• Data Grain: This is an important characteristic of the fact table. As we know, the data grain is the level of detail for the measurements or metrics. In this example, the metrics are at a detailed level. The quantity ordered relates to the quantity of a particular product on a single order, on a certain date, for a specific customer, and procured by a specific sales representative. If we keep the quantity ordered as the quantity of a specific product for each month, then the data grain is different and is at a higher level.
• Fully Additive Measures: Let us look at the attributes order_dollars, extended_cost, and quantity_ordered. Each of these relates to a particular product on a certain date for a specific customer procured by an individual sales representative. In a certain query, let us say that the user wants the totals for the particular product on a certain date, not for a specific customer, but customers in a particular state. Then we need to find all the rows in the fact table relating to all the customers in that state and add the order_dollars, extended_cost, and quantity_ordered to come up with the totals. The values of these attributes may be summed up by simple addition. Such measures are known as fully additive measures. Aggregation of fully additive measures is done by simple addition. When we run queries to aggregate measures in the fact table, we will have to make sure that these measures are fully additive. Otherwise, the aggregated numbers may not show the correct totals.
• Semi-additive Measures: Consider the margin_dollars attribute in the fact table. For example, if the order_dollars is 120 and extended_cost is 100, the margin_percentage is 20. This is a calculated metric derived from the order_dollars and extended_ cost. If you are aggregating the numbers from rows in the fact table relating to all the customers in a particular state, you cannot add up the margin_percentages from all these rows and come up with the aggregated number. Derived attributes such as margin_percentage are not additive. They are known as semi-additive measures. Distinguish semi-additive measures from fully additive measures when you perform aggregations in queries.
• Table Deep, Not Wide: Typically a fact table contains fewer attributes than a dimension table. Usually, there are about 10 attributes or less. But the number of records in a fact table is very large in comparison. Take a very simplistic example of 3 products, 5 customers, 30 days, and 10 sales representatives represented as rows in the dimension tables. Even in this example, the number of fact table rows will be 4500, very large in comparison with the dimension table rows. If you lay the fact table out as a two-dimensional table, you will note that the fact table is narrow with a small number of columns but very deep with a large number of rows.
• Sparse Data: We have said that a single row in the fact table relates to a particular product, a specific calendar date, a specific customer, and an individual sales representative. In other words, for a particular product, a specific calendar date, a specific customer, and an individual sales representative, there is a corresponding row in the fact table. What happens when the data represents a closed holiday and no orders are received and processed? The fact table rows for such dates will not have values for the measures. Also, there could be other combinations of dimension table attributes, values for which the fact table rows will have null measures. Do we need to keep such rows with null measures in the fact table? There is no need for this.

Therefore, it is important to realize this type of sparse data and understand that the fact table could have gaps.

• Degenerate Dimensions: Look closely at the example of the fact table. You find the attributes of order_number and order_line. These are not measures or metrics or facts. Then why are these attributes in the fact table? When you pick up attributes for the dimension tables and the fact tables from operational systems, you will be left with some data elements in the operational systems that are neither facts nor strictly dimension attributes. Examples of such attributes are reference numbers like order numbers, invoice numbers, order line numbers, and so on. These attributes are useful in some types of analyses. For example, you may be looking for an average number of products per order. Then you will have to relate the products to the order number to calculate the average. Attributes such as order_number and order_line in the example are called degenerate dimensions and these are kept as attributes of the fact table.

The Factless Fact Table

Apart from the concatenated primary key, a fact table contains facts or measures. Let us say we are building a fact table to track the attendance of students. For analyzing student attendance, the possible dimensions are student, course, date, room, and professor. The attendance may be affected by any of these dimensions. When you want to mark the attendance relating to a particular course, date, room, and professor, what is the measurement you come up for recording the event? In the fact table row, the attendance will be indicated with the number one. Every fact table row will contain the number one as attendance.

If so, why bother to record the number one in every fact table row? There is no need to do this. The very presence of a corresponding fact table row could indicate the attendance. This type of situation arises when the fact table represents events. Such fact tables really do not need to contain facts. They are “factless” fact tables. The below Figure shows a typical factless fact table.

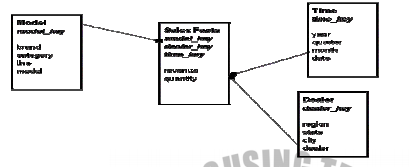
Relationship between Dimension and Fact:

Eg of Fact table records:

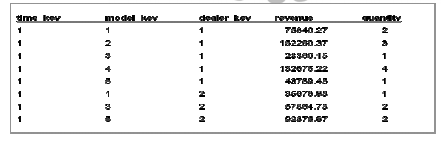
Types of Facts

Fully additive Facts:

• Can be summed across all dimensions
• Stored in a fact table

Examples: revenue, quantity

Eg:

Semi Additive Facts:

• Can be summed across most dimensions but not all
• Examples: Inventory quantities, account balances, or personnel counts Anything that measures a “level”
• Must be careful with ad-hoc reporting
• Often aggregated across the “forbidden dimension” by averaging

Non-Additive Facts:

• Cannot be summed across any dimension
• All ratios are non-additive
• Break down to fully additive components, store them in the fact table

Fact Less Fact table:

•  A fact table with no measures in it
•  Nothing to measure...
•  Except for the convergence of dimensional attributes
•  Sometimes store a “1” for convenience

Examples: Attendance, Customer Assignments, Coverage

Surrogate Keys:

The surrogate keys are simply system-generated sequence numbers. Used generally in two situations

• To replace the use of the primary key(if it is composite)
• To generate unique values

We use this surrogate key both at the Dimension table and Fact table.

Difference between Star and Snow Flake schema

STAR SCHEMA	SNOWFLAKE SCHEMA
Here all dimensions are directly connected to the fact table. Dimension doesn’t contain any hierarchies.	it is just like star schema but dimensions contain sub-dimensions .so dimensional hierarchies are available
Denormalized	Normalized
Less joins, query performance faster	More joins, query performance slow
More memory occupies	Less memory occupies
Business people can easy to understand	Complex to understand
Designed for dwh. OLAP applications	Designed for OLTP more and OLAP less
Fewer tables, consolidated	More tables, elaborated
One to many relationships between fact and dimensions

Slowly Changing Dimensions:

• Dimension source data may change over time
• Relative to fact tables, dimension records change slowly
• Allows dimensions to have multiple 'profiles' overtime to maintain a history
• Each profile is a separate record in a dimension table

Slowly Changing Dimension Types:

Three types of slowly changing dimensions

Type 1:

• Updates existing record with modifications
• Does not maintain a history

Type 2:

• Adds new record
• Does maintain history
• Maintains old record

Type 3:

• Keep old and new values in the existing row
• Requires a design change