Binary Trees in Data Structures

Binary Tree

 A binary trees in data structures T is defined as a finite set of elements, called nodes, such that :

1. T is empty ( called the null tree of empty tree)
2. T contains a distinguished node R, called the root of T and the remaining nodes of T form an order pair of disjoin binary trees T1 and T2.

If T does contain a root R, Then the two trees T1 and T2 are called, respectively the left and right sub trees of R.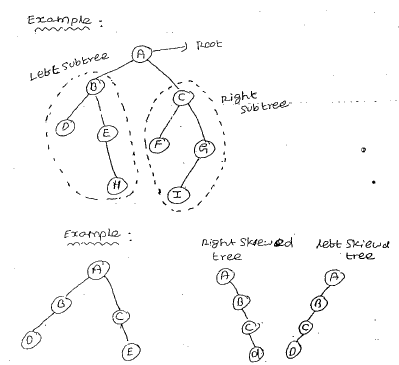        

Differences between a binary tree and a tree in data structures

• A binary tree in data structures can be empty, where as a tree can not
• Each element is a binary has exactly two sub trees (one of both of these sub trees may be empty). Each element in a tree can have any number of sub trees.

  Algebraic expressions Following figure shows some binary trees that represent arithmetic expressions. Each operator (+,-,*,/) may have one or two operands The left operand (if any) is the left sub trees of the operator. The right operand is its right sub tree. The right operand is its right sub tree . The leaf element in an expression tree are either constants or variables. Note that an expression tree contains parenthesis One application of expression trees is in the generation of optimal computer code to evaluate an expression   Example : (a-b)/(Cc*d)+e)

• c*d
• a-b
• 1+e
• 2/3

      Example: (a*b) + (c/d)

1. a*b
2.  c/d
3. 1+2

    Example : ((a+b)+c)+d)    

Properties of binary trees

1. The drawing of every binary tree with n elements, n>0, has exactly n-1 edges.
2. A binary tree of height h, h>=0, has at least hand at most 2^n-1 elements init.

 

 Full binary tree & complete binary tree

A binary tree of height h that contains exactly 2^n-1 elements is called a full binary tree.       The tree T is said to be complete if all its levels, except possible the last, have the maximum number of possible nodes, and if all the nodes at the last level appear as far left as possible.  

Representation of Binary trees

The following are the two ways of representing binary trees

• Array representation
• Linked representation

 

• Array representation

Suppose T is a binary tree that is complete or nearly complete or nearly complete. Then there is an efficient representation of T. This representation uses only a single linear array TREE as follows.

1. The root R of T is stored in TREE[1]
2. If a node N occupies TREE[k]. then the left child is , stored in TREE[2*K] and its right child is stored in TREE[2*(k+1)]

Again , Null is used to indicate an empty sub tree in particular, TREE[1]= NULL indicates that the tree is empty.   This representation schema is quite waste of space when many elements are mission. The array representation is useful only when the number of missing elements is small.

• Linked representation

The most popular way to represent a binary tree is by using links or pointers. Each element is represented by a node. That has exactly two link fields. Let us call these link fields left child and right child. In addition to these two link fields each node has a filed named data. Example:  

Binary  tree traversal

There are three common ways to traversal a binary tree :

• Pre order traversal
• in order traversal
• Post order traversal

Preorder traversal

• Process the root R.
• Traverse the left sub tree of R in preorder
• Traverse the right sub tree of R in preorder.

   

In order Traverse

• Traverse the left sub tree or R in in order
• Process the left R
• Traverse the right sub tree R in in order.

Post order Traversal

• Traverse the left sub tree of R in post order
• Traverse the right sub tree of R in post order
• Process the Root R.

    Algorithm                 Preorder traversal void preorder(Binary Tree Node*t) { // preorder traversal if(t) { printf(“%d”,t- >data);         // visit tree root preorder(t-> leftchild);       // do left sub tree preorder(t-> right child);  // do right sub tree } }   Algorithm In order traversal void inorder (Binary TreeNode   *t) { // Inorder traversal if(t) { inorder(c-> leftchild);  // do left subtree printf(“%d”,t-> data);  // visit tree root inorder(t-> right child); // do right sub tree } }   Algorithm Post order traversal void post order(Binary Tree Node *t) { if(t) { past order(t-> left child);       // do left sub tree past order(t-> right child); // do right sub tree printf(“%d”,t-> data); // visit tree root } }